在自动控制理论中,最负盛名的莫过于PID控制算法了。原理简单,应用广泛,受到很多的工程师们的喜爱。在稚晖君最新的视频BV1jE41137eu中,他设计的’自行车’XUAN的自行车车头无刷电机的控制算法就是PID控制算法。
前言
在过程控制中,按偏差的比例(P)、积分(I)和微分(D)进行控制的PID控制器(亦称PID调节器)是应用最为广泛的一种自动控制器。它具有原理简单,易于实现,适用面广,控制参数相互独立,参数的选定比较简单等优点;而且在理论上可以证明,对于过程控制的典型对象──“一阶滞后+纯滞后”与“二阶滞后+纯滞后”的控制对象,PID控制器是一种最优控制。PID调节规律是连续系统动态品质校正的一种有效方法,它的参数整定方式简便,结构改变灵活(PI、PD、…)。
在工业过程中,连续控制系统的理想PID控制规律为:
u ( t ) = K p ( e ( t ) + 1 T t ∫ 0 t e ( t ) d t + T D d e ( t ) d t ) u(t)=K_p(e(t)+\frac{1}{T_t}\int_0^te(t)dt+T_D\frac{de(t)}{dt})
u ( t ) = K p ( e ( t ) + T t 1 ∫ 0 t e ( t ) d t + T D d t d e ( t ) )
式中,Kp——比例增益,Kp与比例度成倒数关系;
反馈调节
在自动控制原理中,引入反馈调节的主要目的就是为了使得系统更加稳定,增加系统的抗干扰能力,减小稳态误差。
为了能够更好地描述整个系统的各个量之间的关系,像神经网络一样,我们将PID系统看做是一个黑盒模型,将当前输入设为rin(t),输出为rout(t),那么系统误差就是err(t)=rin(t)-rout(t)。
像在稚晖君的”自行车”项目中,把自行车的水平偏移量作为输出rout(t),而无刷电机的输出电流设为rin(t),根据算法竟可能的减小err(t)的值就可以了,这其实并不是一个表面上看起来那么简单的过程。我们来模拟一下这个看似简单的车头控制过程。
比例增益调节(P)
要实现车头转动一定的角度,那么我们首先想到的就是将目标角度与输出角度的差值err(t)按照一定的比例系数K p K_p K p
缺一张流图,下次再画。
根据上图,我们可以知道系统的传递函数为
G ( s ) = 1 T s + 1 G(s)=\frac{1}{Ts+1}
G ( s ) = T s + 1 1
那么该系统的阶跃响应就是
e s s = lim s → 0 s 1 s 1 + K G ( s ) = lim s → 0 1 1 + K T s + 1 = 1 1 + K e_{ss}=\lim_{s\to0}s\frac{\frac{1}{s}}{1+KG(s)}=\lim_{s\to0}\frac{1}{1+\frac{K}{Ts+1}}=\frac{1}{1+K}
e ss = s → 0 lim s 1 + K G ( s ) s 1 = s → 0 lim 1 + T s + 1 K 1 = 1 + K 1
由上式可知误差值并不会随着K p K_p K p K p K_p K p
积分控制(I)
G ( s ) = G 0 ( s ) s k G(s)=\frac{G_0(s)}{s^k}
G ( s ) = s k G 0 ( s )
e s s = lim s → 0 1 s k + s k K G 0 ( s ) s k = lim s → 0 1 K G ( 0 ) = c e_{ss}=\lim_{s\to0}\frac{1}{s^k+s^kK\frac{G_0(s)}{s^k}}=\lim_{s\to0}\frac{1}{KG(0)}=c
e ss = s → 0 lim s k + s k K s k G 0 ( s ) 1 = s → 0 lim K G ( 0 ) 1 = c
通过观察上式可知,如果我们要得到一个稳定的0误差的输出,只需要引入一个1 s k \frac{1}{s^k} s k 1
微分控制(D)
前面我们说到,当我们的K p K_p K p K p K_p K p K p K_p K p
代码实现
虽然从PID为什么能够稳定的控制目标的输出上看起来长篇大论,但是,只要用代码实现前面那个PID的公式就可以了。
位置式PID算法来自CSDN
PID.py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 import timeclass PID : def __init__ (self, P=0.2 , I=0.0 , D=0.0 ): self.Kp = P self.Ki = I self.Kd = D self.sample_time = 0.00 self.current_time = time.time() self.last_time = self.current_time self.clear() def clear (self ): self.SetPoint = 0.0 self.PTerm = 0.0 self.ITerm = 0.0 self.DTerm = 0.0 self.last_error = 0.0 self.int_error = 0.0 self.windup_guard = 20.0 self.output = 0.0 def update (self, feedback_value ): error = self.SetPoint - feedback_value self.current_time = time.time() delta_time = self.current_time - self.last_time delta_error = error - self.last_error if (delta_time >= self.sample_time): self.PTerm = self.Kp * error self.ITerm += error * delta_time if (self.ITerm < -self.windup_guard): self.ITerm = -self.windup_guard elif (self.ITerm > self.windup_guard): self.ITerm = self.windup_guard self.DTerm = 0.0 if delta_time > 0 : self.DTerm = delta_error / delta_time self.last_time = self.current_time self.last_error = error self.output = self.PTerm + (self.Ki * self.ITerm) + (self.Kd * self.DTerm) def setKp (self, proportional_gain ): self.Kp = proportional_gain def setKi (self, integral_gain ): self.Ki = integral_gain def setKd (self, derivative_gain ): self.Kd = derivative_gain def setWindup (self, windup ): self.windup_guard = windup def setSampleTime (self, sample_time ): self.sample_time = sample_time
测试代码
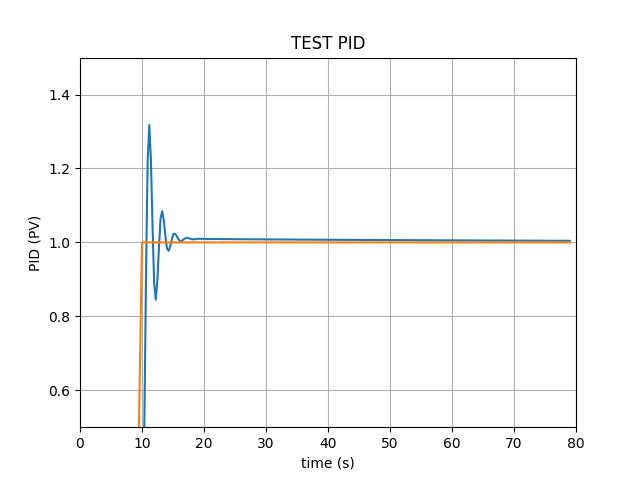
test.py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 import PIDimport timeimport matplotlibmatplotlib.use("TkAgg" ) import matplotlib.pyplot as pltimport numpy as npfrom scipy.interpolate import make_interp_splinedef test_pid (P = 0.2 , I = 0.0 , D= 0.0 , L=100 ): pid = PID.PID(P, I, D) pid.SetPoint=0.0 pid.setSampleTime(0.01 ) END = L feedback = 0 feedback_list = [] time_list = [] setpoint_list = [] for i in range (1 , END): pid.update(feedback) output = pid.output if pid.SetPoint > 0 : feedback +=output if i>9 : pid.SetPoint = 1 time.sleep(0.01 ) feedback_list.append(feedback) setpoint_list.append(pid.SetPoint) time_list.append(i) time_sm = np.array(time_list) time_smooth = np.linspace(time_sm.min (), time_sm.max (), 300 ) feedback_smooth = make_interp_spline(time_list, feedback_list)(time_smooth) plt.figure(0 ) plt.plot(time_smooth, feedback_smooth) plt.plot(time_list, setpoint_list) plt.xlim((0 , L)) plt.ylim((min (feedback_list)-0.5 , max (feedback_list)+0.5 )) plt.xlabel('time (s)' ) plt.ylabel('PID (PV)' ) plt.title('TEST PID' ) plt.ylim((1 -0.5 , 1 +0.5 )) plt.grid(True ) plt.show() if __name__ == "__main__" : test_pid(1.2 , 1 , 0.001 , L=80 )
测试结果
总结
上面的PID运行原理我理解的或者描述可能不太准确,但是公式和代码是没问题的。如果想要更详细的视频解析,可以在哔哩哔哩搜一下PID控制。