ChatGPT问世以来，引起了广泛的关注。GPT(Generative Pre-Trained Transformer)模型，其中的Transformer就是使用的网络，在去年的文献检索课上我还在打趣的说，未来是属于Transformer的，没想到这一天来的这么快。

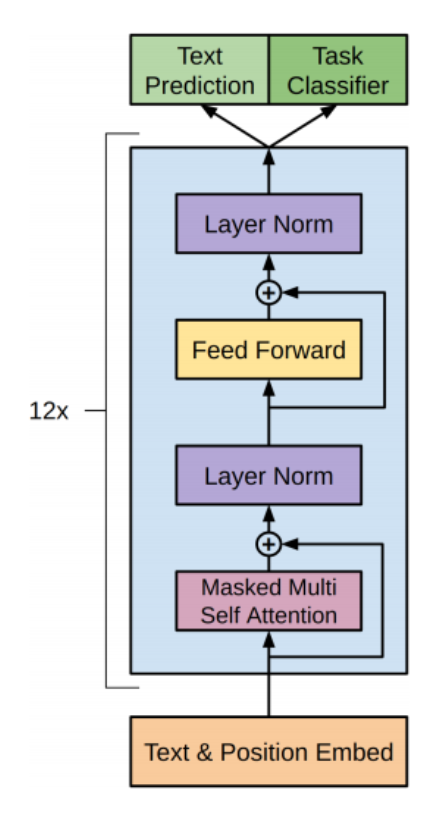
GPT模型网络结构

先放一个GPT网络的模型结构：
nano-gpt-2023-06-19-02-49-48

Attention原理

假设我们现在有这样两组初始数据，身高（Key）和体重（Value）：

身高(Key) 体重(Value)
175 70
178 76
180 81

假如现在来了一个179的帅小伙，想要预测他的体重应该怎么办？
自然的，依据初始数据分布，我们一般认为他的体重会在76和81之间，那么我们可以简单的取平均值：
$$
Weight(179) = \frac{76+81}{2} = 78.5
$$
也就是78.5，这就是我们的预测结果。我们注意到上面的0.5就是我们分配给它们的注意力权重，但是175这个数据我们并没有利用上，那么我们应该如何合理的分配权重呢？这就是Attention机制要解决的问题。

假设使用$\alpha(q,k_i)$来表示$q$与$k$对应的Attention权重，那么Weight(q)就可以表示为：
$$
Weight(q)=\sum_{i=1}^{n}\alpha(q,k_i)v_i
$$
其中$\alpha$需要进行归一化，最容易想到的当然是Hardmax，也就是
$$
Weight(q)=Hardmax(\alpha(q,k_i))v_i=\sum_{i=1}^{n}\frac{|q - k_i|}{\sum_{j=1}^{n}|q - k_j|}v_i
$$

但是，很明显，Hardmax的导数或者说梯度，并不连续，没有办法求解，所以我们需要使用Softmax来进行归一化，以高斯核函数为例，也就是
$$
Weight(q)=Softmax(\alpha(q,k_i))v_i=\frac{exp(-\frac{1}{2}(q-k_i)^2)}{\sum_{j=1}^{n}exp(-\frac{1}{2}(q-k_i)^2)}v_i
$$

那么，当Loss为交叉熵($L=-ln(\frac{e^{f_yi}}{\sum_{j}e^j})$)的时候，神经网络在对$\alpha(q,k_i)$求导的时候，就可以使用链式法则，也就是
$$
\frac{\partial \alpha(q,k_i)}{\partial q} = \frac{\partial (-ln(\frac{e^{f_yi}}{\sum_{j}e^j}))}{\partial f_{yi}} = P_{f_{yi}} - 1
$$

额，虽然结果简单，但是推导过程异常复杂，有兴趣的小伙伴可以自己推导一下。知乎

结论就是，只要将算出来的概率的向量对应的真正结果的那一维减1，就是Loss的梯度了。

其中，高斯核函数用来计算两个向量的相似度，得到的结果称之为注意力分数，也就是Attention Score，也就是上面的$P_{f_{yi}}$。而Softmax用来归一化，得到的结果称之为注意力权重，也就是Attention Weight，也就是上面的$\alpha(q,k_i)$。

当然，注意力分数表示方法不止只有高斯核函数，还有很多种，在多维的情况下，我们可以使用其他方式表示

  1. 点积
    $$
    \alpha(q,k_i)=qk_i^T
    $$

  2. 缩放点积
    $$
    \alpha(q,k_i)=\frac{qk_i^T}{\sqrt{d}}
    $$

  3. 加性
    $$
    \alpha(q,k_i)=v^Ttanh(W_1q+W_2k_i)
    $$

点积可以通过矩阵乘法直接并行地计算所有位置之间的相似度。这使得缩放点积注意力在实际应用中具有较高的计算效率。由于点积和缩放点积都是线性的，所以无法表示非线性的关系，所以加性注意力就应运而生了。

同时，为了缓解注意力分数的不稳定性，也就是梯度消失的问题，我们可以使用缩放点积，也就是除以$\sqrt{d}$，其中$d$表示向量的维度。

那么，假设我们有多行的$q$,$k_i$，那么将这些行组合成一个矩阵Q，K，最终，注意力模型可以表示为
$$
Attention(Q)=softmax(\frac{QK^T}{\sqrt{di}})V
$$

当QKV是同一个矩阵的时候，也就是Self-Attention的时候，我们可以简化为
$$
Attention(X)=softmax(\frac{XX^T}{\sqrt{di}})X
$$

在Transformer中，我们还需要定义三个可以训练的权重矩阵，分别是$W_Q$、$W_K$、$W_V$，其中的X，就是我们的输入，也就是
$$
Attention(X)=softmax(\frac{XW_Q(XW_K)^T}{\sqrt{di}})XW_V
$$

那么，在PyTorch中，我们可以这样实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import torch
import torch.nn as nn

def a_norm(Q, K):
    m = torch.matmul(Q, K.transpose(2,1).float())
    m /= torch.sqrt(torch.tensor(Q.shape[-1]).float())
    
    return torch.softmax(m , -1)

def attention(Q, K, V):
    #Attention(Q, K, V) = norm(QK)V
    a = a_norm(Q, K) #(batch_size, dim_attn, seq_length)
    
    return  torch.matmul(a,  V) #(batch_size, seq_length, seq_length)

class AttentionBlock(torch.nn.Module):
    def __init__(self, dim_val, dim_attn):
        super(AttentionBlock, self).__init__()
        self.value = nn.Linear(dim_val, dim_val)
        self.key = nn.Linear(dim_val, dim_attn)
        self.query = nn.Linear(dim_val, dim_attn)
    
    def forward(self, x, kv = None):
        if(kv is None):
            #Attention with x connected to Q,K and V (For encoder)
            return attention(self.query(x), self.key(x), self.value(x))
        
        #Attention with x as Q, external vector kv as K an V (For decoder)
        return attention(self.query(x), self.key(kv), self.value(kv))

Multi-Head Attention

实际上，在Transformer模型中，使用Muti-Head机制代替我们刚才讲解的single self-attention，它的公式表示：
$$
MultiHead(Q,K,V)=Concat(head_1,…,head_h)W^O \
head_i=Attention(X)
$$

因为权重矩阵$W^Q_i$,$W^K_i$,$W^V_i$​各不相同，结果也各不相同，因此我们说每个头的关注点各有侧重。最后，将每个头计算出的 single self-attention进行concat，通过总的权重矩阵W^O决定对每个头的关注程度，从而能够做到在不同语境下对相同句子进行不同理解。

一句话总结：Attention是将query和key映射到同一高维空间中去计算相似度，而对应的multi-head attention把query和key映射到高维空间$\alpha$的不同子空间$(\alpha1,\alpha2,…)$中去计算相似度。

那么，在PyTorch中，我们可以这样实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import torch
import torch.nn as nn

class MultiHeadAttentionBlock(torch.nn.Module):
    def __init__(self, dim_val, dim_attn, n_heads):
        super(MultiHeadAttentionBlock, self).__init__()
        self.heads = []
        for i in range(n_heads):
            self.heads.append(AttentionBlock(dim_val, dim_attn))
        
        self.heads = nn.ModuleList(self.heads)
        self.dropout = nn.Dropout(0.1)
        self.fc = nn.Linear(n_heads * dim_val, dim_val, bias = False)
        
    def forward(self, x, kv = None):
        a = []
        for h in self.heads:
            a.append(h(x, kv = kv))
            
        a = torch.stack(a, dim = -1) #combine heads
        a = a.flatten(start_dim = 2) #flatten all head outputs
        
        a = self.dropout(a)
        x = self.fc(a)
        
        return x

Layer Normalization

在每个block中，最后出现的是Layer Normalization，其作用是规范优化空间，加速收敛。

$$
LayerNorm(x)=\alpha\frac{x-\mu}{\sqrt{\sigma^2 + \xi}}+\beta
$$

当我们使用梯度下降算法做优化时，我们可能会对输入数据进行归一化，但是经过网络层作用后，我们的数据已经不是归一化的了。随着网络层数的增加，数据分布不断发生变化，偏差越来越大，导致我们不得不使用更小的学习率来稳定梯度。Layer Normalization 的作用就是保证数据特征分布的稳定性，将数据标准化到ReLU激活函数的作用区域，可以使得激活函数更好的发挥作用。

Normalization有两种方法，Batch Normalization和Layer Normalization。关于两者区别不再详述。

那么，在PyTorch中，我们可以这样实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import torch
import torch.nn as nn

class LayerNormBlock(torch.nn.Module):
    def __init__(self, dim_val, dim_attn, n_heads):
        super(LayerNormBlock, self).__init__()
        self.attn = MultiHeadAttentionBlock(dim_val, dim_attn, n_heads)
        self.norm = nn.LayerNorm(dim_val)
        
    def forward(self, x):
        a = self.attn(x)
        x = self.norm(a + x)
        
        return x

Position-wise Feed Forward

每一层经过attention之后，还会有一个FFN，这个FFN的作用就是空间变换。FFN包含了2层linear transformation层，中间的激活函数是ReLu。

$$
FFN(x)=max(0,xW_1+b_1)W_2+b_2
$$

其实，FFN的加入引入了非线性(ReLu激活函数)，变换了attention output的空间, 从而增加了模型的表现能力。把FFN去掉模型也是可以用的，但是效果差了很多。

那么，在PyTorch中，我们可以这样实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import torch
import torch.nn as nn

class PoswiseFeedForwardNet(torch.nn.Module):   # 输入和输出形状不变
    def __init__(self, dim_val, dim_attn):
        super(PoswiseFeedForwardNet, self).__init__()
        self.fc = nn.Sequential(
            nn.Linear(dim_val, dim_attn, bias=False),
            nn.ReLU(),
            nn.Linear(dim_attn, dim_val, bias=False)
        )
        self.layernorm = nn.LayerNorm(dim_val)

    def forward(self, inputs):
        residual = inputs
        output = self.fc(inputs)
        return self.layernorm(output + residual)

GPT模型结构，以GPT-2为例

我们只需要将上述的模块组合起来，就可以得到GPT-2的结构了。

那么，在PyTorch中，我们可以这样实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import torch
import torch.nn as nn

class DecoderLayer(nn.Module):
    def __init__(self, dim_val, dim_attn, n_heads, n_layers):
        super(DecoderLayer, self).__init__()
        self.layer = LayerNormBlock(dim_val, dim_attn, n_heads) # 包含了MultiHeadAttentionBlock和LayerNormBlock
        self.pos_ffn = PoswiseFeedForwardNet(dim_val, dim_attn)
        
    def forward(self, x):
        x = self.layer(x)
        x = self.pos_ffn(x)
            
        return x

class Decoder(nn.Module):
    def __init__(self, dim_val, dim_attn, n_heads, n_layers):
        super(Decoder, self).__init__()
        self.layers = nn.ModuleList([DecoderLayer(dim_val, dim_attn, n_heads, n_layers) for _ in range(n_layers)])
        
    def forward(self, x):
        for layer in self.layers:
            x = layer(x)
            
        return x

class GPT(nn.Module):
    def __init__(self, dim_val, dim_attn, n_heads, n_layers):
        super(GPT, self).__init__()
        self.decoder = Decoder(dim_val, dim_attn, n_heads, n_layers)
        self.fc = nn.Linear(dim_val, dim_val, bias = False)
        
    def forward(self, x):
        x = self.decoder(x)
        x = self.fc(x)

        return x

完了？并没有，还有几个重要的问题，就是如何将文本转换成输入向量？GPT的训练方式是什么？这些问题，我们将在下一篇文章中讨论。